Question

A population of beetles are growing according to a linear growth model. The initial population (week 0) is

P0=6, and the population after 8 weeks is P8=86 Find an explicit formula for the beetle population after n weeks.

After how many weeks will the beetle population reach 236?

Answer 1

The number of weeks it will take for the beetle population to reach 236 is 28.75.

Explanation:

If a quantity starts at size P₀ and grows by d every time period, then the

quantity after n time periods can be determined using explicit form:

`P_(n) = P_(0) + d \cdot n`

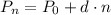
Here,

d = the common difference, i.e. the amount that the population changes each time n is increased by 1.

In this case it is provided that the original population of beetle was:

P₀ = 6; (week 0)

And the population after 8 weeks was,

P₈ = 86

Compute the value of d as follows:

`P_(8) = P_(0) + d \cdot 8\\86=6+8d\\86-6=8d\\80=8d\\d=10`

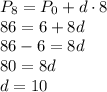
Thus, the explicit formula for the beetle population after n weeks is:

`P_(n)=P_(0)+8n`

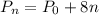
Compute the number of weeks it will take for the beetle population to reach 236 as follows:

`P_(n)=P_(0)+8n\\\\236=6+8n\\\\8n=236-6\\\\8n=230\\\\n=28.75`

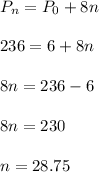
Thus, the number of weeks it will take for the beetle population to reach 236 is 28.75.