Answer:
The maximum height reached by the rocket is of 938.56 feet.
Explanation:
The height y, after x seconds, is given by a equation in the following format:

If a is negative, the maximum height is:
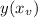
In which

In this question:
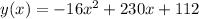
So
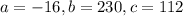
Then

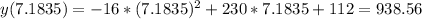
The maximum height reached by the rocket is of 938.56 feet.