Question

After a long study, tree scientists conclude that a eucalyptus tree will grow at the rate of 0.5 6/ (t+4)3 feet per year, where t is the time (in years)

(a) Find the number of feet that the tree will grow in the second year.
(b) Find the number of feet the tree will grow in the third year.
(c) The total number of feet grown during the second year is_____________ ft.

Answer 1

a) 0.5367feet

b) 0.5223feet

c) 0.7292feet

Explanation:

Given the rate at which an eucalyptus tree will grow modelled by the equation 0.5+6/(t+4)³ feet per year, where t is the time (in years).

The amount of growth can be gotten by integrating the given rate equation as shown;

`\int\limits {0.5 + (6)/((t+4)^(3) ) } \, dt \\= \int\limits {0.5} \, dt + \int\limits(6)/((t+4)^(3) ) } \, dx } \, \\= 0.5t +\int\limits {6u^(-3) } \, du \ where \ u = t+4 \ and\ du = dt\\= 0.5t + 6*(u^(-2) )/(-2) + C\\= 0.5t-3u^(-2) +C\\= 0.5t-3(t+4)^(-2) + C`

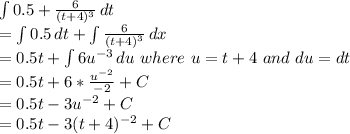
a) The number of feet that the tree will grow in the second year can be gotten by taking the limit of the integral from t =1 to t = 2

`\int\limits^2_1 {0.5 + (6)/((t+4)^(3) ) } \, dt = [0.5t-3(t+4)^(-2)]^2_1\\= [0.5(2)-3(2+4)^(-2)] - [0.5(1)-3(1+4)^(-2)]\\= [1-3(6)^(-2)] - [0.5-3(5)^(-2)]\\ = [1-(1)/(12)] - [0.5-(3)/(25) ]\\= (11)/(12)-(1)/(2)+(3)/(25)\\ = 0.9167 - 0.5 + 0.12\\= 0.5367feet`

b) The number of feet that the tree will grow in the third year can be gotten by taking the limit of the integral from t =2 to t = 3

`\int\limits^3_2 {0.5 + (6)/((t+4)^(3) ) } \, dt = [0.5t-3(t+4)^(-2)]^3_2\\= [0.5(3)-3(3+4)^(-2)] - [0.5(2)-3(2+4)^(-2)]\\= [1.5-3(7)^(-2)] - [1-3(6)^(-2)]\\ = [1.5-(3)/(49)] - [1-(1)/(12) ]\\ = 1.439 - 0.9167\\= 0.5223feet`

c) The total number of feet grown during the second year can be gotten by substituting the value of limit from t = 0 to t = 2 into the equation as shown

`\int\limits^2_0 {0.5 + (6)/((t+4)^(3) ) } \, dt = [0.5t-3(t+4)^(-2)]^2_0\\= [0.5(2)-3(2+4)^(-2)] - [0.5(0)-3(0+4)^(-2)]\\= [1-3(6)^(-2)] - [0-3(4)^(-2)]\\ = [1-(1)/(12)] - [-(3)/(16) ]\\= (11)/(12)+(3)/(16)\\ = 0.9167 - 0.1875\\= 0.7292feet`