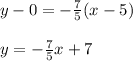Question

Una escalera está apoyada sobre una pared a 4,33 m de altura y forma con el piso un ángulo de 60°. a) Calcula el largo de la escalera. b) Si el punto B correspondiera a (5,0) y el punto a correspondiera a (0,7). Halla la ecuación de la recta que pasa por los dos puntos, es decir la escalera.

Answer 1

a) 5,00 m

b) y = - (7/5)x + 7

Explanation:

The stairs and the wall forms a rectangle triangle. The wall is the opposite side respect to the angle which stairs forms with ground (I attached an image below of the situation).

a) To find the length of stairs you use the following trigonometric relation:

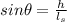`sin\theta=(h)/(l_s)` (1)

h: height in which the stairs touch the wall = 4,33 m

ls: length of the stairs

θ: angle between ground and stairs = 60°

You solve the equation (1) for ls:

`l_s=(h)/(sin\theta)=(4,33m)/(sin60\°)=4,99m\approx5,00m`

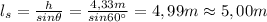
b) The line equation is given by:

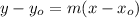`y-y_o=m(x-x_o)` (2)

Firs, you calculate the slope by using the equation (2):

`m=(0-7)/(5-0)=-(7)/(5)`

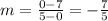
Next, you use one of the point, say B, an you replace this points for yo and xo:

`y-0=-(7)/(5)(x-5)\\\\y=-(7)/(5)x+7`