Question

The height, h in feet, a ball with reach when thrown in the ais is a function of time, t, in seconds,given by the equation h(t)=-16t2+35t+10. Find, to the nearest tenth, the maximum height, in feet, the ball will reach. The time when it reached its maximum height. How many seconds after the ball is thrown it will hit the ground?

Answer 1

The maximum height the ball will reach is 29,141 feet.

The time when it reached its maximum height is 1.094 seconds.

2,443 seconds after throwing the ball, it will touch the ground.

Explanation:

The function h (t) = - 16t² + 35t + 10 is a quadratic function of the form f (x) = ax² + bx + c, where a = -16, b = 35 and c = 10. To calculate the maximum height, you must then find the maximum of the function. In other words, Quadratic functions have a maximum (if a <0) or a minimum (if a> 0). This point is the vertex of the parabola.

The vertex coordinate on the x axis can be calculated by:

`x=(-b)/(2*a)`

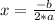
The value of the vertex on the y axis is obtained by substituting the value of "x vertex" in the function f (x), that is, by calculating f (
`(-b)/(2*a)`).

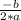In this case, where h (
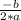`(-b)/(2*a)`) is the maximum height:

`t=(-b)/(2*a)=(-35)/(2*(-16)) =1.09375`≅ 1.094 seconds

So: h(1.094)= -16*1.094² + 35*1.094 + 10

h(1.094)=29.151

The maximum height the ball will reach is 29,141 feet.

The time when it reached its maximum height is 1.094 seconds.

To calculate the number of seconds after the ball is thrown it will hit the ground, you must calculate the roots of the quadratic function. For this you must apply:

`x1,x2=\frac{-b+-\sqrt{b^(2)-4*a*c } }{2*a}`

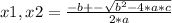
where x1, x2 are the two roots of the function f(x)=a*x² +b*x + c

In this case:

`t1,t2=\frac{-35+-\sqrt{35^(2)-4*(-16)*10 } }{2*(-16)}`

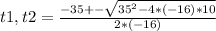
Solving, you get t1=-0.256 and t2=2.443

Since the time cannot be negative, 2,443 seconds after throwing the ball, it will touch the ground.