Question

Is​ f(x) continuous at x equals 4​? Why or why​ not? A. ​No, f(x) is not continuous at x equals 4 because ModifyingBelow lim With x right arrow 4 f (x )does not exist. B. ​Yes, f(x) is continuous at x equals 4 because f (4 )exists. C. ​No, f(x) is not continuous at x equals 4 because f (4 )is undefined. D. ​Yes, f(x) is continuous at x equals 4 because ModifyingBelow lim With x right arrow 4 f (x )equals f (4 ).

Answer 1

Corrected Question

Is the function given by:

`f(x)=\left\{\begin{array}{ccc}(1)/(4)x+1 &x\leq 4\\4x-11&x>4\end{array}\right` ​

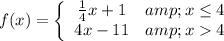
continuous at x=4​? Why or why​ not? Choose the correct answer below.

Answer:

(D) ​Yes, f(x) is continuous at x = 4 because
`Lim_(x \to 4)f(x)=f(4)`

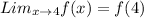
Explanation:

Given the function:

`f(x)=\left\{\begin{array}{ccc}(1)/(4)x+1 &x\leq 4\\4x-11&x>4\end{array}\right`

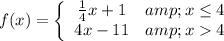
A function to be continuous at some value c in its domain if the following condition holds:

• f(c) exists and is defined.

• 
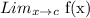  `Lim_(x \to c)$ f(x)` exists.

• 
  `f(c)=Lim_(x \to c)$ f(x)`

At x=4

• 
  `f(4)=(1)/(4)*4+1=2`

• 
  `Lim_(x \to 4)f(x)=2`

Therefore:
`Lim_(x \to 4)f(x)=f(4)=2`

By the above, the function satisfies the condition for continuity.

The correct option is D.