Question

According to a report released by CIBC entitled "Women Entrepreneurs: Leading the Charge," the average age for Canadian businesswomen in 2008 was 41. In the report, there was some indication that researchers believed that this mean age will increase. Suppose now, a few years later, business researchers in Canada want to test to determine if, indeed, the mean age of Canadian businesswomen has increased. The researchers randomly sample 97 Canadian businesswomen and ascertain that the sample mean age is 43.4. From past experience, it is known that the population standard deviation is 8.95. Test to determine if the mean age of Canadian businesswomen has increased using a 1% level of significance. What is the p-value for this test? What is the decision? If the null hypothesis is rejected, is the result substantive?

Answer 1

We conclude that the mean age of Canadian businesswomen has increased.

Explanation:

We are given that according to a report released by CIBC entitled "Women Entrepreneurs: Leading the Charge," the average age for Canadian businesswomen in 2008 was 41.

The researchers randomly sample 97 Canadian businesswomen and ascertain that the sample mean age is 43.4. From past experience, it is known that the population standard deviation is 8.95.

Let
`\mu` = mean age of Canadian businesswomen.

So, Null Hypothesis,
`H_0` :
`\mu`
`\leq` 41 {means that the mean age of Canadian businesswomen has decreased or remained same}

Alternate Hypothesis,
`H_A` :
`\mu` > 41 {means that the mean age of Canadian businesswomen has increased}

The test statistics that would be used here One-sample z-test statistics because we know about population standard deviation;

T.S. =
`(\bar X-\mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where,
`\bar X` = sample mean age of Canadian businesswomen = 43.4

`\sigma` = population standard deviation = 8.95

n = sample of Canadian businesswomen = 97

So, the test statistics =
`(43.4-41)/((8.95)/(√(97) ) )`

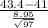
= 2.64

The value of z test statistic is 2.64.

Also, P-value of the test statistics is given by;

P-value = P(Z > 2.64) = 1 - P(Z < 2.64)

= 1 - 0.99585 = 0.00415

Now, at 1% significance level the z table gives critical value of 2.33 for right-tailed test.

Since our test statistic is more than the critical value of z as 2.64 > 2.33, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region due to which we reject our null hypothesis.

Therefore, we conclude that the mean age of Canadian businesswomen has increased.