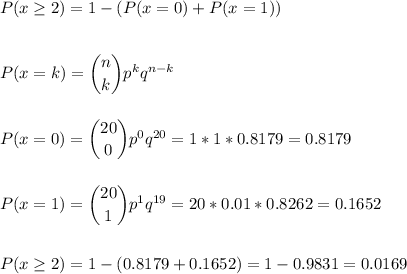Question

5. A company sells small, colored binder clips in packages of 20 and offers a money-back guarantee if two or more of the clips are defective. Suppose a clip is defective with probability 0.01, independently of other clips. Let X denote the number of defective clips in a package of 20. (a) The distribution of the random variable X is (choose one) (i) binomial (ii) hypergeometric (iii) negative binomial (iv) Poisson. (b) Specify the value of the parameter(s) of the chosen distribution and find the probability that a package sold will be refunded.

Answer 1

a) Binomial.

b) n=20, p=0.01, k≥2

The probability hat a package sold will be refunded is P=0.0169.

Explanation:

a) We know that

• the defective probability is constant and independent.
• the sample size is bigger than one subject.

The most appropiate distribution to represent this random variable is the binomial.

b) The parameters are:

• Sample size (amount of clips in the package): n=20
• Probability of defective clips: p=0.01.
• number of defective clips that trigger the money-back guarantee: k≥2

The probability of the package being refunded can be calculated as:

`P(x\geq2)=1-(P(x=0)+P(x=1))\\\\\\P(x=k) = \dbinom{n}{k} p^(k)q^(n-k)\\\\\\P(x=0) = \dbinom{20}{0} p^(0)q^(20)=1*1*0.8179=0.8179\\\\\\P(x=1) = \dbinom{20}{1} p^(1)q^(19)=20*0.01*0.8262=0.1652\\\\\\P(x\geq2)=1-(0.8179+0.1652)=1-0.9831=0.0169`