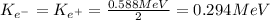Answer:
Ke- = Ke+ = 0.294MeV
Step-by-step explanation:
To fins the kinetic energy of both electron and positron you use the following formula, for the case of annihilation of one electron an positron:
2
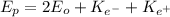 (1)
(1)
Ep: photon energy = 0.804MeV
Eo: rest energy of one electron (and positron) = 0.51MeV
Ke-: kinetic energy of electron
Ke+: kinetic energy of positron
You replace the values of Ep and Eo in the equation (1):
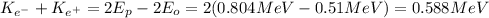
Iy you assume both positron and electron have the same speed, then, the kinetic energy of them are equal, and the kinetic energy of each one is: