Question

A parabola has a focus of (6,–6) and a directrix of y = –2. Which of the following could be the equation of the parabola?

Answer 1

`-8(y+4) =(x-6)^(2)`

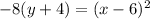
Explanation:

The standard form of a parabola is given by the following equation:

`(x-h)^(2) =4p(y-k)`

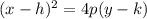
Where the focus is given by:

`F(h,k+p)`

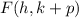
The vertex is:

`V=(h,k)`

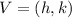
And the directrix is:

`y-k+p=0`

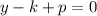
Now, using the previous equations and the information provided by the problem, let's find the equation of the parabola.

If the focus is (-6,6):

`F=(h,k+p)=(6,-6)`

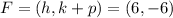
Hence:

`h=6\\\\k+p=-6\hspace{10}(1)`

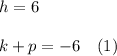
And if the directrix is
`y=-2` :

`-2-k+p=0\\\\k-p=-2\hspace{10}(2)`

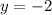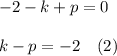
Using (1) and (2) we can build a 2x2 system of equations:

`k+p=-6\hspace{10}(1)\\k-p=-2\hspace{10}(2)`

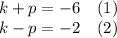
Using elimination method:

(1)+(2)

`k+p+k-p=-6+(-2)\\\\2k=-8\\\\k=-(8)/(2)=-4\hspace{10}(3)`

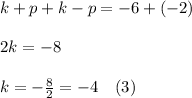
Replacing (3) into (1):

`-4+p=-6\\\\p=-6+4\\\\p=-2`

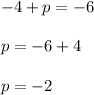
Therefore:

`(x-6)^(2) =4(-2)(y-(-4)) \\\\(x-6)^(2) =-8(y+4)`

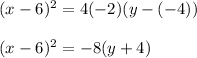
So, the correct answer is:

Option 3