Answer:
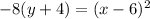
Explanation:
The standard form of a parabola is given by the following equation:
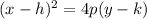
Where the focus is given by:
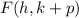
The vertex is:
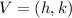
And the directrix is:
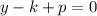
Now, using the previous equations and the information provided by the problem, let's find the equation of the parabola.
If the focus is (-6,6):
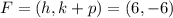
Hence:

And if the directrix is
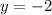 :
:
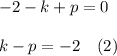
Using (1) and (2) we can build a 2x2 system of equations:
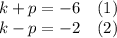
Using elimination method:
(1)+(2)
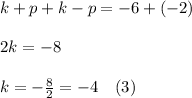
Replacing (3) into (1):
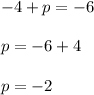
Therefore:
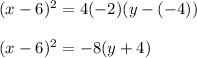
So, the correct answer is:
Option 3