Complete Question
Let A be an n x n matrix, b be a nonzero vector, and x_0 be a solution vector of the system Ax = b. Show that x is a solution of the non-homogeneous system Ax = b if and only if y = x - x_0 is a solution of the homogeneous system Ay = 0.
Answer:
Explanation:
From the question we are told that
A is an n × n matrix
b is a zero vector
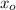 us the solution vector of
us the solution vector of
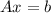
Which implies that
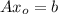
So first we show that
if
 is the solution matrix of
is the solution matrix of
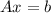
and
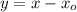 is the solution of
is the solution of
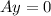
Then
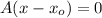
=>

=>

Secondly to show that
if
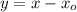 is the solution of
is the solution of
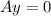
then x is the solution of the non-homogeneous system
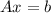
Now we know that
 is the solution of
is the solution of
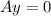
So
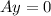
=>
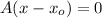
=>

=>

=>
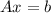
Thus this has been proved