Question

The energy, E, of a body of mass m moving with speed v is given by the formula below. The speed is nonnegative and less than the speed of light, c which is constant. Use lower case letters here. E = mc^2 (1/Squareroot1 - v^2/c^2 - 1)

(a) Find E/m = c^2Squareroot1 - v^2/c^2 - c^2/1 - v^2/c^2 what is the sign of this partial? Positive negative
(b) Find E/v =?

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

a

`(\delta E)/(\delta m)= c^2 [\frac{1}{\sqrt{1 - (v^2)/(c^2) } } -1 ]`

b

`(\delta E)/(\delta V) = \frac{mc^3 v}{(c^2 - v^2 )^{(3)/(2) }}`

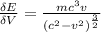
Explanation:

From the question we are given

`E = mc^2 [\frac{1}{\sqrt{1 - (v^2)/(c^2) } }- 1 ]`

So we are asked to find
`(\delta E)/(\delta m)`

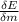
Now this is mathematically evaluated as

`(\delta E)/(\delta m) = (\delta )/(\delta m) [mc^2 ( \frac{1}{\sqrt{1 - (v^2)/(c^2) } } -1 )]`

`= c^2 [\frac{1}{\sqrt{1 - (v^2)/(c^2 ) } } -1 ] (\delta m)/(\delta m)`

`= c^2 [\frac{1}{\sqrt{1 - (v^2)/(c^2) } } -1 ]`

Also we are asked to find
`(\delta E)/(\delta V)`

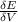
Now this is mathematically evaluated as

`(\delta E)/(\delta V) = (\delta )/(\delta v ) [mc^2 ( \frac{1}{\sqrt{1 - (v^2)/(c^2) } } - 1 )]`

`(\delta E)/(\delta V) = mc^2 [(\delta )/(\delta v) ((c)/(√(c^2 -v^2) ) - 1 )]`

`= mc^2 [c* [(\delta )/(\delta v) (c^2 - v^2 )^{-(1)/(2) }] - 0]`

`= mc^3 [- (1)/(2) (c^2 - v^2 )^{-(3)/(2) } * (-2v)]`

`= \frac{mc^3 v}{(c^2 - v^2 )^{(3)/(2) }}`