Answer:
![Range = [24, 375]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/1z8lm6cwiyj2ae8zltgr1r9gy56ir4np63.png)
Explanation:
Given
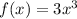
![Domain = [2,5]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/opmb8o8zoxb7q3is3wckexxqme0u52759g.png)
Required
Find the Range
The range is calculated by solving for f(2) and f(5). In other words, the range is calculated when x is 2 and x is 5
When x = 2;
f(2) is as follows;
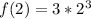
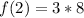
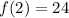
When x = 5;
f(5) is as follows;
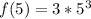
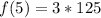
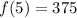
Hence, the range of the function is [24, 375]