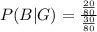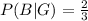2 Answers

Jeremy Seekamp · Answer 1 · 2021-04-12T08:25:06+0000

Complete Question

Calculating conditional probability

The usher at a wedding asked each of the 80 guests whether they were a friend of the bride or of the groom.

Here are the results:

Bride :29

Groom :30

BOTH : 20

Given that a randomly selected guest is a friend of the groom, find the probability they are a friend of the bride.

P (bride | groom)

Answer:

The probability is
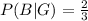
P(B|G) = (2)/(3)

Explanation:

The sample size is
n = 80

The friend of the groom are
G = 30

The friend of the groom are
B = 29

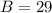
The friend of both bride and groom are
Z = 20

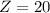
The probability that a guest is a friend of the bride is mathematically represented as

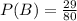
P(B) = (29)/(80)

The probability that a guest is a friend of the groom is mathematically represented as

P(G) = (30)/(80)

The probability that a guest is both a friend of the bride and a friend of the groom is mathematically represented as

$P(B \ n \ G) = (20)/(80)$

Now

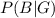P(B|G) is mathematically represented as

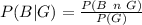
$P(B|G) = (P(B \ n \ G))/(P(G))$

Substituting values

P(B|G) = ((20)/(80) )/((30)/(80) )

P(B|G) = (2)/(3)

Please log in or register to add a comment.