Question

A student used multiple regression analysis to study how family spending (y) is influenced by income

(x1), family size (x2), and additionsto savings(x3). The variables y, x1, and x3 are measured in thousands
of dollars. The following results were obtained.
ANOVA
df SS
Regression 3 45.9634
Residual 11 2.6218
Total
Coefficients Standard Error
Intercept 0.0136
x1
0.7992 0.074
x2
0.2280 0.190
x3
-0.5796 0.920
a. Write out the estimated regression equation for the relationship between the variables. (1
mark)
b. Compute coefficient of determination. What can you say about the strength of this
relationship? (3 marks)
c. Carry out a test to determine whether y is significantly related to the independent variables.
Use a 5% level of significance. (3 marks)
d. Carry out a test to see if x3 and y are significantly related. Use a 5% level of significance.

Answer 1

Explanation:

Hello!

Given the variables

Y: family spending

X₁: income of a family

X₂: family size

X₃: additions to savings of a family

And the regression output (see attachment)

The population model is Y= α + β₁X₁ + β₂X₂ + β₃X₃

a)

To write the estimated regression equation of the relationship between the variables you have to use the information given in the regression output. Under the column "coefficients", the value that corresponds to "intercept" is the estimation of the y-intercept (a), the value under X₁ corresponds to the estimation for the slop for the variable "income of the family" (b₁), under X₂ is the estimation of the slope for the variable "family size" (b₂) and under X₃ is the estimation for the slope corresponding to the variable "additions to savings" (b₃)

The estimated regression equation is:

^Y= a + b₁X₁ + b₂X₂ + b₃X₃

^Y= 0.0136 + 0.7992X₁ + 0.2280X₂ -0.5796X₃

b)

Using the SS information you can calculate the coefficient of determination as:

SStotal= SSReg+SSError= 45.9634+2.6218= 48.5852

`R^2= (SS_(Reg))/(SS_(Total)) = (45.9634)/((48.5852)) = 0.946`

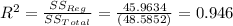
R²= 94.6%

This means that 94.6% of the variability of the average family spending is explained jointly by the family income, the family size and the addition to saving under the estimated model ^Y= 0.0136 + 0.7992X₁ + 0.2280X₂ -0.5796X₃

c)

The hypotheses are:

H₀: β₁= β₂= β₃= 0

H₁: At least one βi≠0 ∀ i=1, 2, 3

α: 0.05

The statistic for the multiple regression is

`F=(MS_(Reg))/(MS_(Error)) ~~F_{Df_(Reg);Df_(Error)}`

`MS_(Reg)= (SS_(reg))/(Df_(Reg))= (45.9634)/(3) = 15.32`

`MS_(Error)= (SS_(Error))/(Df_(Error)) = (2.6218)/(11) = 0.238`

`F_(H_0)= (MS_(Reg))/(MS_(Error))= (15.32)/(0.238)= 64.37`

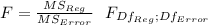
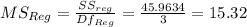
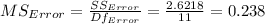
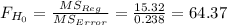
p-value < .00001

At a 5% significance level, there is enough evidence to reject the null hypothesis. This means that the family income, family size and the addition to savings modify jointly the average spending of families.

d.

Individual tests:

There are two possible statistics to test the significance of each independent variable:
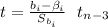`t= (b_i-\beta_i )/(S_(b_i)) ~~t_(n-3)` ∀ i= 1, 2, 3, or
`F=(MS_(X_i))/(MS_(Error)) ~F_{Df_(X_i); Df_(Error\\)}`

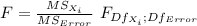
Since the output doesn't give us the information of the individual ANOVA, you have to use the t-test (Df: n-3= 12-3= 9) for these hypotheses. Using the p-value approach. the decision rule for the three hypothesis will be:

If p-value ≤ α ⇒ Reject null hypothesis.

If p-value > α ⇒ Do not reject the null hypothesis.

1)

H₀: β₁ = 0

H₁: β₁ ≠ 0

α: 0.05

`t_(H_0)= (b_1-\beta_1 )/(Sb_1)= (0.7992-0)/(0.074)= 10.8`

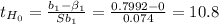
p-value < .00001 ⇒ Decision is to reject the null hypothesis.

2)

H₀: β₂ = 0

H₁: β₂ ≠ 0

α: 0.05

`t_(H_0)= (b_2-\beta_2 )/(Sb_2)= (0.2280-0)/(0.190)= 1.2`

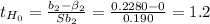
p-value: 0.260773 ⇒ The decision is to not reject the null hypothesis.

3)

H₀: β₃ = 0

H₁: β₃ ≠ 0

α: 0.05

`t_(H_0)= (b_3-\beta_3 )/(Sb_3)= (-0.5796-0)/(0.920)= -0.63`

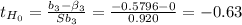
p-value: 0.544355 ⇒ The decision is to not reject the null hypothesis.

So, at a 5% significance level, it seems that the three independent variables influence jointly the variation on the average spending of the families, but looking at them separately, only the income of the families seems to affect their spending habits significantly while the family size or their addition to savings don't seem to have major effect over their spending habits.

I hope this helps!