Answer:
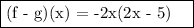
Explanation:
Given:
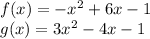
Solve for:
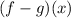
Solution:
Perform the subtraction:
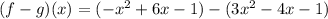
Eliminate the parenthesis (notice the change in sign of some components):
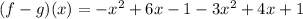
Rearrange the expression:
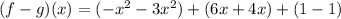
Simplify the expression:
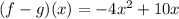
Perform the inverse of associative property:
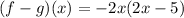
Hope this helps!
:)