Answer:
x-intercept: x=24
DOMAIN: (0,24) where x∈Natural Numbers
RANGE: (0,12) where y∈Natural Numbers
Explanation:
Remain money = y
Number of games = x
Given function:
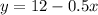
x-intercept:
x-intecept is the value of x where y becomes zero.
Substitute y=0 in the given equation:
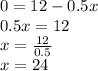
Domain:
Domain is a set of all possible values of x.
x= No. of games (So x cannot be negative)
y= Remain Amount (So y cannot be negative)
So the minimum value of x is 0 because x cannot be negative.
Maximum value of x is the value for which y doesn't become negative. For any value of x>24, y <0 which is not possible.
So maximum value of x is 24
DOMAIN: (0,24) where x∈Natural Numbers
Range:
Range is a set of all outcomes of y for all possible values of x.
For x=0 , y =12
for x=24 , y = 0
So
RANGE: (0,12) where y∈Natural Numbers