Answer:
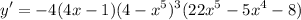
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Distributive Property
Algebra I
- Terms/Coefficients
- Factoring
Calculus
Derivatives
Derivative Notation
Derivative of a constant is 0
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Derivative Rule [Product Rule]:
![\displaystyle (d)/(dx) [f(x)g(x)]=f'(x)g(x) + g'(x)f(x)](https://img.qammunity.org/2021/formulas/mathematics/high-school/s1om3rzcnorfu9si84gajpl5k6jeoialwk.png)
Derivative Rule [Chain Rule]:
![\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)](https://img.qammunity.org/2021/formulas/mathematics/college/ljowxevzhh8dk8mfdheam579ywk5jvteyi.png)
Explanation:
Step 1: Define
Identify
y = (4x - 1)²(4 - x⁵)⁴
Step 2: Differentiate
- Product Rule:
^4 + (4x - 1)^2(d)/(dx)[(4 - x^5)^4]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/dphqn3qd1efacdcwddbfyrhh7on4emtkv7.png)
- Chain Rule [Basic Power Rule]:
![\displaystyle y' = [2(4x - 1)^(2 - 1) \cdot (d)/(dx)[(4x - 1)]](4 - x^5)^4 + (4x - 1)^2[4(4 - x^5)^(4 - 1) \cdot (d)/(dx)[(4 - x^5)]]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/stvykdgm9qzmd8fa3vwj4sqo7pluw5ss15.png)
- Simplify:
![\displaystyle y' = [2(4x - 1) \cdot (d)/(dx)[(4x - 1)]](4 - x^5)^4 + (4x - 1)^2[4(4 - x^5)^3 \cdot (d)/(dx)[(4 - x^5)]]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/7e4cjiumeqgerfous41g2tjhd6n708na0j.png)
- Basic Power Rule:
^4 + (4x - 1)^2[4(4 - x^5)^3 \cdot -5x^(5 - 1)]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/1qvwtr488s97mrvoq27g2powbxh4owf99q.png)
- Simplify:
^4 + (4x - 1)^2[4(4 - x^5)^3 \cdot -5x^4]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/i8nfut2vs3uw9bxsrkt6nuspn0fkx8o55f.png)
- Multiply:
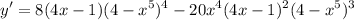
- Factor:
![\displaystyle y' = 4(4x - 1)(4 - x^5)^3 \bigg[ 2(4 - x^5) - 5x^4(4x - 1) \bigg]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/xba9xmj4m88adyh2mn1uj3e1b216aiga8f.png)
- [Distributive Property] Distribute 2:
![\displaystyle y' = 4(4x - 1)(4 - x^5)^3 \bigg[ 8 - 2x^5 - 5x^4(4x - 1) \bigg]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/kjfprklpb382690kqxqm9neilzoabzc4nm.png)
- [Distributive Property] Distribute -5x⁴:
![\displaystyle y' = 4(4x - 1)(4 - x^5)^3 \bigg[ 8 - 2x^5 - 20x^5 + 5x^4 \bigg]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/vpq5mr1148q9wrajqg244ftnoqsfesz2aj.png)
- [Brackets] Combine like terms:
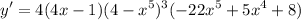
- Factor:
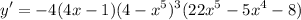
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Derivatives
Book: College Calculus 10e