Question

A small block with a mass of 0.120 kg is attached to a cord passing through a hole in a frictionless, horizontal surface (Fig. 6.34). The block is originally revolving at a distance of 0.40 m from the hole with a speed of 0.70 m/s. The cord is then pulled from below, shortening the radius of the circle in which the block revolves to 0.10 m. At this new distance, the speed of the block is observed to be 2.80 m/s.

(a) What is the tension in the cord in the original situation when the block has speed v = 0.70 m/s? (b) What is the tension in the cord in the final situation when the block has speed v = 2.80 m/s? (c) How much work was done by the person who pulled on the cord?

Answer 1

a) 0.147 N

b) 9.408 N

c) 9.261 N

Step-by-step explanation:

The tension on the cord is the only force keeping the block in circular motion, thus representing the entirety of its centripetal force
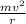`(mv^(2) )/(r)`. Plugging in values for initial and final states and we get answers for a and b. The work done by the person causes the centripetal force to increase, and thus is the difference between the final tension and the initial tension.