Question

An athletics squad trains on a long straight track with dots marked at 10m intervals. The coach sets out cones on some of the dots for the squad's sprint training drills. She wants the squad to be able to run any distance which is a multiple of 10m, up to some maximum distance which depends on the number of cones.

Explain why it is not possible to place four cones A, B, C, D, in a line so that each multiple of 10m up to 70m can be run between two of the cones.

Answer 1

There are 6 ways to run 10 m between two cones of the four cones giving a maximum available distance to run as 60 meters

Explanation:

The parameters given are

Distance between two cones = 10 m

Number of cones = 4

Therefore, number of ways to choose two 10 m distances (distance between two cones) from the four cones =
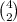`\binom{4}{2}` = 6

Hence there are only six 10 m distances to run between two cones which gives a maximum distance available to run as 60 m.