Question

The triceps muscle in the back of the upper arm is primarily used to extend the forearm. Suppose this muscle in a professional boxer exerts a force of 1.95 × 103 N with an effective perpendicular lever arm of 3.1 cm, producing an angular acceleration of the forearm of 125 rad/s2. What is the moment of inertia of the boxer's forearm?

Answer 1

I = 0.483 kgm^2

Step-by-step explanation:

To know what is the moment of inertia I of the boxer's forearm you use the following formula:

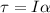`\tau=I\alpha` (1)

τ: torque exerted by the forearm

I: moment of inertia

α: angular acceleration = 125 rad/s^2

You calculate the torque by using the information about the force (1.95*10^3 N) and the lever arm (3.1 cm = 0.031m)

`\tau=Fr=(1.95*10^3N)(0.031m)=60.45J`

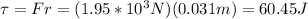
Next, you replace this value of τ in the equation (1) and solve for I:

`I=(\tau)/(\alpha)=(60.45Kgm^2/s ^2)/(125rad/s^2)=0.483 kgm^2`

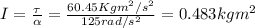
hence, the moment of inertia of the forearm is 0.483 kgm^2