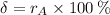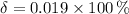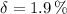Answer:
a)
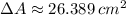 , b)
, b)
 , c)
, c)
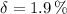
Explanation:
a) The area of the circular disk is modelled after this expression:
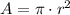
The total differential is given by the following formula:
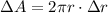
The maximum absolute error in the calculated area of the disk is:

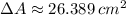
b) The relative error is given by:
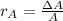


c) The percentage error is: