Question

The red giant Betelgeuse has a surface temperature of 3000 K and is 600 times the diameter of our sun. (If our sun were that large, we would be inside it!) Assume that it radiates like an ideal blackbody.a) If Betelgeuse were to radiate all of its energy at the peak-intensity wavelength, how many photons per second would it radiate?b) Find the ratio of the power radiated by Betelgeuse to the power radiated by our sun (at 5800 K).

Answer 1

Step-by-step explanation:

a )

Radius of the sun = .69645 x 10⁹ m .

600 times = 600 x .69645 x 10⁹ m

= 4.1787 x 10¹¹ m .

surface area A = 4π (4.1787 x 10¹¹)²

= 219.317 x 10²²

energy radiated E = σ A Τ⁴

= 5.67 x 10⁻⁸ x 219.317 x 10²² x (3000)⁴

= 100695 x 10²⁶ J

To know the wavelength of photon emitted

`\lambda_mT= b`

`\lambda_m= (b)/(T)`

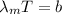
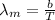
= 2.89777 x 10⁻³ / 3000

= 966 nm

= 1275 /966 eV

1.32 x 1.6 x 10⁻¹⁹ J

= 2.112 x 10⁻¹⁹ J

No of photons radiated = 100695 x 10²⁶ / 2.112 x 10⁻¹⁹

= 47677.5 x 10⁴⁵

= .476 x 10⁵⁰ .

b )

energy radiated by our sun per second

E₂ = σ A 5800⁴

energy radiated by Betelgeuse per second

E₁ = σ x 600²A x 3000⁴

E₁ / E₂ = σ x 600²A x 3000⁴ / σ A 5800⁴

= 36 X 10⁴ x 3⁴ x 10¹² / 58⁴ x 10⁸

= 25.76 x 10⁸ x 10⁻⁵

= 25760 times .