Here is the correct question.
The manufacturer of a smart watch claims that individuals who pay attention to how many steps they take per day will inadvertently take more steps per day than individuals who pay no attention to how many steps they take per day. To investigate this claim, the manufacturer conducts a study to estimate the difference in the mean number of steps taken by those that pay attention to how many steps they take per day and those that do not. To do so, 40 volunteers are recruited. Half of the volunteers are randomly assigned to receive a smart watch and are taught how to use it to track their steps. The other half of the volunteers are given a wristband to wear, but are not informed that the wristband is tracking their steps. The volunteers are monitored for 30 days. The mean and standard deviation of the number of steps taken per day are computed for each group. Here are the data:


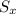
Pay attention 20 10,244 1,580
Do not pay attention 20 8.,648 2,350
Which of the following is a 99% confidence interval for the difference in the mean number of steps taken by all people like these that do and do not pay attention to the number of steps they take per day using df - 19 ?
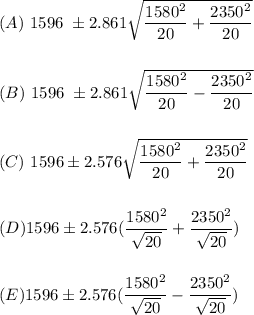
Answer:

Explanation:
Given that :
significance level
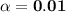
From the Given data;
Using Excel with the function : TINV(0.01,19);
Critical value t* = 2.861
The margin of error can now be represented by the illustration:
Margin of error =
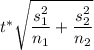
Lower Limit =

Upper Limit =
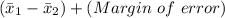
Thus; the confidence interval for the difference in the mean number of steps taken by all people like these that do and do not pay attention to the number of steps they take per day using df - 19 is:
