Question

Formamide decomposes at high temperature. If 0.186 mol of formamide (HCONH2) dissociates in a 2.16 L flask at 400 K, what are the concentrations of all species present at equilibrium at 400 K? (hint: calculate concentrations first) (b) What is the total pressure in the container at equilibrium?

Answer 1

a) [COHNH₂] = 0.001 mol/L, [NH₃] = [CO] = 0.085 mol/L

b) 5.59 atm

Step-by-step explanation:

a) The decomposition reaction of formamide is the following:

COHNH₂(d) ⇆ NH₃(g) + CO(g)

The equilibrium constant of the reaction above is:

`K_(c) = ([NH_(3)][CO])/([COHNH_(2)]) = 4.84 (400 K)`

The initial concentration of formamide is:

`C_{COHNH_(2)} = (\eta)/(V) = (0.186 moles)/(2.16 L) = 0.086 mol/L`

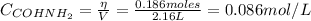
Where: η is the number of moles and V is the volume

Now, in the equilibrium the concentration of all species is:

COHNH₂(d) ⇆ NH₃(g) + CO(g)

0.086 - x x x

`K_(c) = ([NH_(3)][CO])/([COHNH_(2)]) = (x*x)/(0.086 - x)`

`4.84*(0.086 - x) -x^(2) = 0`

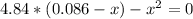
By solving the above equation for x we have:

x = 0.085 mol/L = [NH₃] = [CO]

[COHNH₂] = 0.086 - 0.085 = 0.001 mol/L

Therefore, the concentrations of all species present at equilibrium at 400 K is [NH₃] = [CO] = 0.085 mol/L and [COHNH₂] = 0.001 mol/L.

b) To find the total pressure in the container we need to find first the constant Kp as follows:

`K_(p) = K_(c)*RT^(\Delta n)`

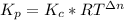
Where R is the gas constant = 0.082 Latm/(Kmol), T is the temperature = 400 K and Δn = 1

`K_(p) = K_(c)*RT^(\Delta n) = 4.84*(0.082*400)^(1) = 158.8`

Now, the total pressure is:

`p_(T) = p_{COHNH_(2)} + p_{NH_(3)} + p_(CO)`

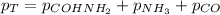
The pressure of COHNH₂ can be found using Ideal Gas Law:

`P = (nRT)/(V) = (0.186 moles*0.082 L*atm/(K*mol)*400 K)/(2.16 L) = 2.82 atm`

Using the equilibrium constant we can find the pressure of NH₃ and CO:

COHNH₂(d) ⇆ NH₃(g) + CO(g)

2.82 - x x x

`K_(p) = \frac{P_{NH_(3)}*P_(CO)}{P_{COHNH_(2)}}`

`158.8*(2.82 - x) - x^(2) = 0`

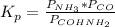
By solving the above equation for x we have:

`x = P_{NH_(3)} = P_(CO) = 2.77 atm`

`P_{COHNH_(2)} = 2.82 - 2.77 = 0.05 atm`

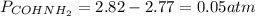
Thus, the total pressure is:

`p_(T) = p_{COHNH_(2)} + p_{NH_(3)} + p_(CO) = (0.05 + 2.77 + 2.77) atm = 5.59 atm`

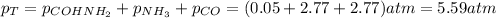
Hence, the total pressure in the container at equilibrium is 5.59 atm.

I hope it helps you!