Answer:
d = 41.91 m
Step-by-step explanation:
In order to calculate the distance traveled by the train while superman passes it, you write the equations of motion for both superman and train:
For train, you have a motion with constant speed. You write the equation of motion of the position of the front of the train:
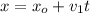 (1)
(1)
xo: initial position of the front of the train = 500m
v1: speed of the train = 50km/h
For superman, you take into account that the motion is an accelerated motion (you assume superman is at the origin of coordinates):
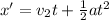 (1)
(1)
v2: initial speed of superman = 100km/h
a: acceleration = 10m/s^2
When superman passes the train, both positions x and x' will be equal. Hence, you equal the equations (1) and (2) and you calculate the time t. But before you convert the units of the velocities v1 and v2 to m/s:

Thus, you equal x=x'
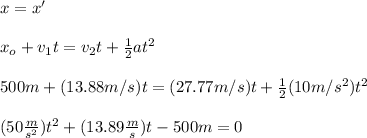
You solve the last equation for t by using the quadratic formula:

You only use t1 = 3.02s because negative times do not have physical meaning.
Next, you replace this value of t in the equation (1) to calculate the position of the train (for when superman just passed it):

x is the position of the front of the train, then, the dstance traveled by the train is:
d = 541.91m - 500m = 41.91 m