Question

Suppose a company's revenue function is given by R(q) = - q^3 + 220q^2 and its cost function is given by C(q) = 500 + 13q, where q is hundreds of units sold/produced, while R(q) and C(q) are in total dollars of revenue and cost, respectively.

A) Find a simplified expression for the marginal profit function. (Be sure to use the proper variable in your answer.)
MP(q) =
B) How many items (in hundreds) need to be sold to maximize profits? (Round your answer to two decimal places.)

Answer 1

A) MP(q) = -3q² + 440q - 13

B) 146.64 units.

Explanation:

The profit function is given by the revenue minus the cost function:

`P(q) = R(q) - C(q)\\P(q) = -q^3+220q^2-500-13q`

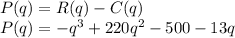
A) The Marginal profit function is the derivate of the profit function as a function of the quantity sold:

`P(q) = -q^3+220q^2-500-13q\\MP(q) = (dP(q))/(dq) \\MP(q)=-3q^2+440q-13`

B) The value of "q" for which the marginal profit function is zero is the number of items (in hundreds) that maximizes profit:

`MP(q)=0=-3q^2+440q-13\\q=(-440\pm √(440^2-(4*(-3)*(-13))) )/(-6)\\q'=146.64\\q'' = - 0.03`

Therefore, the only reasonable answer is that 146.64 hundred units must be sold in order to maximize profit.