Question

Real Estate One conducted a recent survey of house prices for properties located on the shores of Tawas Bay. Data on 26 recent sales, including the number of bathroom, square feet and bedrooms are below.

Selling Price Baths Sq Ft Beds
160000 1.5 1776 3
170000 2 1768 3
178000 1 1219 3
182500 1 1568 2
195100 1.5 1125 3
212500 2 1196 2
245900 2 2128 3
250000 3 1280 3
255000 2 1596 3
258000 3.5 2374 4
267000 2.5 2439 3
268000 2 1470 4
275000 2 1678 4
295000 2.5 1860 3
325000 3 2056 4
325000 3.5 2776 4
328400 2 1408 4
331000 1.5 1972 3
344500 2.5 1736 3
365000 2.5 1990 4
385000 2.5 3640 4
395000 2.5 1918 4
399000 2 2108 3
430000 2 2462 4
430000 2 2615 4
454000 3.5 3700 4
Action:
Use the data above and multiple regression to produce a model to predict the average sale price from other variables. Comment on the following:
a. Regression equation
b. R, R2 and 1-R2, adjusted R2
c. Standard error of estimate
d. Report the t's for each value and the corresponding p-values
e. Overall test of hypothesis and decision
f. Use a .05 level of significance. Cite which variables are significant and which are not significant, based on the t values and p values for each independent variable.

Answer 1

Explanation:

Hello!

Given the data for the variables:

Y: Selling price of a house on the shore of Tawas Bay

X₁: Number of bathrooms of a house on the shore of Tawas Bay.

X₂: Square feet of a house on the shore of Tawas Bay.

X₃: Number of bedrooms of a house on the shore of Tawas Bay.

The multiple regression model is Y= α + β₁X₁ + β₂X₂ + β₃X₃ + εi

a. Using software I've entered the raw data and estimated the regression coefficients:

^α= a= -5531.01

Represents the mean selling price of the houses when 0 bathrooms, 0 square feet and 0 bedrooms.

^β₁= b₁= -1386.21

Represents the modification of the mean selling price of the houses when the number of bathrooms increases in one unit and the square feet and number of bedrooms remain unchanged.

^β₂= b₂= 60.28

Represents the modification of the mean selling price of the houses when the square feet increase in one unit and the number of bathrooms and bedrooms remain unchanged.

^ β₃= b₃= 54797.08

Represents the modification of the mean selling price of the houses when the number of bedrooms increase in one unit and the number of bathrooms and square feet of the houses remain unchanged.

^Y= -5531.01 -1386.21X₁ + 60.28X₂ + 54797.08X₃

b)

R²= 0.55

R²Aj= 0.49

The coefficient of determination gives you an idea of how much of the variability of the dependent variable (Y) is due to the explanatory variables. Each time you add another explanatory variable to the regression the coefficient increases regarding of real contribution of the new variable. This could lead to thinking (wrongly) that the new variables are good to explain the dependent variable.

The adjusted coefficient of determination is a correction made to the raw coefficient of determination to have a more unbiased estimation of the effect the independent variables have over the dependent variable.

⇒ As you can see both coefficient are around 50%, which means that these explanatory variables

c)

The standard error estimate, this is the estimate of the population variance of the errors. In the ANOVA is represented by the Mean Square of the errors (MME)

Se²= MME= 3837640577.01

Se= 61948.6931

d) and f)

For the hypotheses tests for each slope the t- and p-values are:

α: 0.05

β₁:
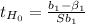`t_(H_0)= (b_1-\beta_1 )/(Sb_1)` t= -0.06; p-value: 0.9528 ⇒ Do not reject H₀, the test is not significant.

β₂:
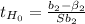`t_(H_0)= (b_2-\beta_2 )/(Sb_2)` t= 2.56; p-value: 0.0180 ⇒ Reject H₀, the test is significant.

β₃:
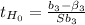`t_(H_0)= (b_3-\beta_3 )/(Sb_3)` t= 2.28; p-value: 0.0326 ⇒ Reject H₀, the test is significant.

e)

H₀: β₁= β₂= β₃

H₁: At least one βi is different from the others ∀ i=1, 2, 3

α: 0.05

F= 9.03

p-value: 0.0004

⇒ Reject H₀, the test is significant.

I hope it helps!