Question

How many moles of gas are contained in 22.41 liters at 101.325 kPa and 0ᴼC? (Note: use Ideal Gas Law, PV = nRT) a 2.5 mole b 1.5 mole c 1.0 mole d 2.0 mole

Answer 1

1 mole of gas is contained in 22.41 liters at 101.325 kPa and 0ᴼC

Step-by-step explanation:

Ideal gases are a simplification of real gases that is done to study them more easily. It is considered to be formed by point particles, do not interact with each other and move randomly. It is also considered that the molecules of an ideal gas, in themselves, do not occupy any volume.

The pressure, P, the temperature, T, and the volume, V, of an ideal gas, are related by a simple formula called the ideal gas law:

P*V = n*R*T

where P is the gas pressure, V is the volume that occupies, T is its temperature, R is the ideal gas constant, and n is the number of moles of the gas.

In this case:

• P= 101.325 kPa= 1 atm
• V= 22.41 L
• n=?

• R= 0.082
  `(atm*L)/(mol*K)`

• T= 0°C= 273 °K

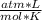
Replacing:

1 atm*22.41 L=n* 0.082
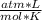`(atm*L)/(mol*K)`*273 K

Solving:

`n=(1 atm*22.41 L)/(0.082(atm*L)/(mol*K) *273 K)`

n=1 mole

1 mole of gas is contained in 22.41 liters at 101.325 kPa and 0ᴼC

Answer 2

Therefore, 1.00 mole of the gas is present in the container.

Step-by-step explanation:

The following data were obtained from the question:

Volume (V) = 22.41L

Temperature (T) = 273K

Pressure (P) = 101.325 kPa

Gas constant (R) = 8.31 L.kPa/mol.K.

Number of mole (n) =...?

The number of mole of the gas in the container can obtained by applying the ideal gas equation as illustrated below:

PV = nRT

Divide both side by RT

n = PV /RT

n =101.325 x 22.41 / 8.31 x 273

n = 1.00 mole.

Therefore, 1.00 mole of the gas is present in the container.