Question

A motorboat travels 50 miles downstream in a river, then turns around and travels back to its starting point. The total trip takes 8 hours. The rate of the current in the river is 2miles per hour. Remembering that distance = rate x time, what is the rate of the motorboat in calm water? HELP NEEDED ASAP

A. 0.31 miles per hour
B. 2.08 miles per hour
C. 12.5 miles per hour
D. 12.8 miles per hour

Answer 1

12.8

Explanation:

Answer 2

The speed of the boat in calm water is 12.8 miles per hour.

Explanation:

While going downstream the speed of the boat is "x + 2", where x is the speed in calm water, while going upstream the speed of the boat is "x - 2". He made a trip that had two legs, each with a distance of 50 miles, therefore, the sum of the times it took him to complete each leg must be equal to the total time of the trip.

`speed = (distance)/(time)\\\\time = (distance)/(speed)`

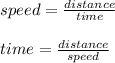
For the upstream:

`time_(up) = (50)/(x - 2)`

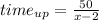
For the downstream:

`time_(d) = (50)/(x + 2)`

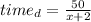
The sum of each of these times must be equal to "8 h", therefore:

`8 = time_(up) + time_(d)\\\\8 = (50)/(x - 2) + (50)/(x + 2)\\\\8 = (50*(x+2) + 50*(x - 2))/((x-2)*(x+2))\\\\8*(x-2)*(x+2) = 50*x + 100 + 50*x - 100\\\\8*(x^2 - 4) = 100*x\\\\8*x^2 - 100*x - 32 = 0\\\\x^2 - 12.5*x - 4 = 0\\\\x_(1,2) = (-(-12.5) \pm √((-12.5)^2 - 4*(1)*(-4)))/(2)\\\\x_(1,2) = (12.5 \pm √(156.25 + 16))/(2)\\\\x_(1,2) = (12.5 \pm √(172.25))/(2)\\\\x_(1,2) = (12.5 \pm 13.124)/(2)\\\\x_1 = 12.812\\\\x_2 = -0.312`

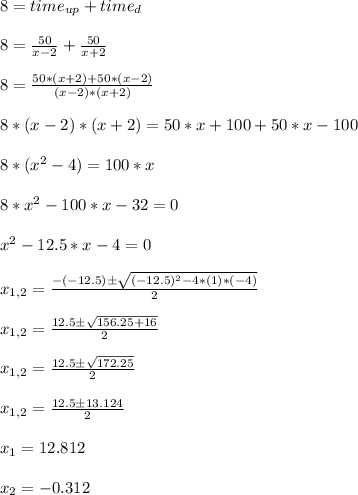
Since the speed can't be negative in this context, the only possible answer is 12.812 mph.