Question

Use the Factor Theorem to examine the polynomial p(x)=6x4+x3−45x2+26x+24. Which binomial is a factor of p(x)?

2x+3
(3x-2)
(2x-1)
(3x−4)

Answer 1

(D) 3x−4

Explanation:

Factor Theorem

Given a polynomial P(x) and a linear function x-a, If P(a)=0, then the linear function x-a is a factor of P(a).

In Option A:

`L$inear Function =2x+3\\Set 2x+3=0$\\x=-(3)/(2) \\p(x)=6x^4+x^3-45x^2+26x+24\\p(-(3)/(2))=6(-(3)/(2))^4+(-(3)/(2))^3-45(-(3)/(2))^2+26(-(3)/(2))+24\\\\p(-(3)/(2))=-89.25`

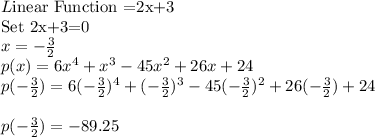
In Option B

`L$inear Function =3x-2\\Set 3x-2=0$\\x=(2)/(3) \\p(x)=6x^4+x^3-45x^2+26x+24\\p((2)/(3))=6((2)/(3))^4+((2)/(3))^3-45((2)/(3))^2+26((2)/(3))+24\\\\p((2)/(3))=22.8`

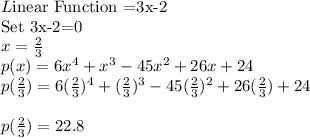
In Option C

`L$inear Function =2x-1\\Set 2x-1=0$\\x=(1)/(2) \\p(x)=6x^4+x^3-45x^2+26x+24\\p((1)/(2) )=6((1)/(2) )^4+((1)/(2) )^3-45((1)/(2) )^2+26((1)/(2) )+24\\\\p((1)/(2) )=26.25`

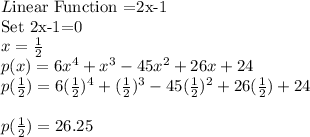
In Option D

`L$inear Function =3x-4\\Set 3x-4=0$\\x=(4)/(3) \\p(x)=6x^4+x^3-45x^2+26x+24\\p((4)/(3) )=6((4)/(3))^4+((4)/(3) )^3-45((4)/(3) )^2+26((4)/(3))+24\\\\p((4)/(3) )=0`

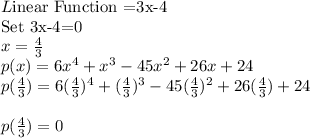
We can see that only Option D: 3x−4 gives a result of 0. Therefore, by the factor theorem, it is a factor of the polynomial.