Question

Near the top of the Citigroup Center building in New York City, there is an object with mass of 4.8 x 105 kg on springs that have adjustable force constants. Its function is to dampen wind-driven oscillations of the building by oscillating at the same frequency as the building is being driven-the driving force is transferred to the object, which oscillates instead of the entire building X 50%

Part (a) What effective force constant, in N/m, should the springs have to make them oscillate with a period of 1.2 s? k = 9.5 * 106 9500000 X Attempts Remain 50%
Part (b) What energy, in joules, is stored in the springs for a 1.6 m displacement from equilibrium?

Answer 1

The force constant is
`k =1.316 *10^(7) \ N/m`

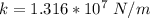
The energy stored in the spring is
`E = 1.68 *10^(7) \ J`

Step-by-step explanation:

From the question we are told that

The mass of the object is
`M = 4.8*10^(5) \ kg`

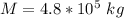
The period is
`T = 1.2 \ s`

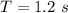
The period of the spring oscillation is mathematically represented as

`T =2 \pi \sqrt{ (M)/(k)}`

where k is the force constant

So making k the subject

`k = (4 \pi ^2 M )/(T^2)`

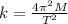
substituting values

`k = (4 (3.142) ^2 (4.8 *10^(5)) )/((1.2)^2)`

`k =1.316 *10^(7) \ N/m`

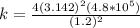
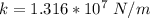
The energy stored in the spring is mathematically represented as

`E = (1)/(2) k x^2`

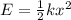
Where x is the spring displacement which is given as

`x = 1.6 \ m`

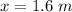
substituting values

`E = (1)/(2) (1.316 *10^(7)) (1.6)^2`

`E = 1.68 *10^(7) \ J`