Question

Lightbulbs of a certain type are advertised as having an average lifetime of 750 hours. The price of these bulbs is very favorable, so a potential customer has decided to move forward with a purchase agreement unless it can be demonstrated that the true average lifetime is smaller than what is advertised. A random sample of 50 lightbulbs was selected, the lifetime of each bulb determined, and the appropriate hypotheses were tested using computer software, which gave the following results.

Variable N Mean St Dev SEMean Z P-Value
lifetime 50 738.44 38.20 5.40 -2.14 0.016
1. What conclusion would be appropriate for a significance level of.05?
2. What significance level would you recommend?

Answer 1

a) For this case since the p value is lower than the significance level of 0.05 we have enough evidence to reject the null hypothesis and we can conclude that the true mean is significantly lower than 750 hours

b) We can use a significance level minimum of 2% in order to ensure the conditions in favor to the alternative hypothesis and then the potential customer will decide to move forward with a purchase witht his condition.

Explanation:

For this case we have the following info given after conduct the following system of hypothesis:

Null hypothesis:
`\mu \geq 750`

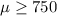
Alternative hypothesis:
`\mu< 750`

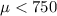
The output is:

Variable N Mean St Dev SEMean Z P-Value

lifetime 50 738.44 38.20 5.40 -2.14 0.016

For this case the statistic calculated was:

`z = -2.14`

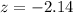
And the p value calculated is:

`p_v =p(z<-2.14) = 0.016`

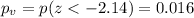
Part a

For this case since the p value is lower than the significance level of 0.05 we have enough evidence to reject the null hypothesis and we can conclude that the true mean is significantly lower than 750 hours

Part b

We can use a significance level minimum of 2% in order to ensure the conditions in favor to the alternative hypothesis and then the potential customer will decide to move forward with a purchase witht his condition.