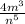Question
Which expression is equivalent to
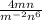 . Assuming
. Assuming
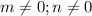
Answer:
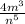
Explanation:
Given
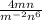
Required:
Simplify
To simplify this, we start by splitting each individual function
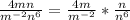
From laws of indices
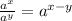
SO, the above expression can also be expressed the same way
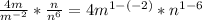
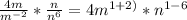
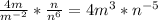
From laws of indices,
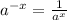
So,
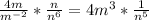
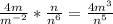
Hence,
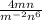 is equivalent to
is equivalent to