Question

Identify the type of data​ (qualitative/quantitative) and the level of measurement for the following variable. Explain. The average mass (in grams )of a sample of rocks collected in the waters of a region.

1. Are the data qualitative or​ quantitative?
A. Qualitative, because descriptive terms are used to measure or classify the data.
B. Quantitative, because descriptive terms are used to measure or classify the data.
C. Qualitative, because numerical values, found by either measuring or counting, are used to describe the data.
D. Quantitative, because numerical values, found by either measuring or counting, are used to describe the data.
2. What is the data set's level of measurement?
A. Ratio, because the differences in the data can be meaningfully measured, and the data have a true zero point.
B. Interval, because the differences in the data can be meaningfully measured, but the data do not have a true zoro point.
C. Nominal, because the data are categories or labels that cannot be ranked.
D. Ordinal, because the data are categories or labels that can be ranked.
3. What is the probability of randomly selecting a diamond from a standard 52-card deck?The probability of selecting a diamond is 0.25.
4. Use the contingency table to complete parts a) through d) below.
Event A Event B
Event C 10 11
Event D 3 4
Event E 14 8
A) Determine the probability of P(AIC).
B) Determine the probability of P(CIA).
C) Determine the probability of P(BE).
5. Use the contingency table to complete parts a) through d) below.
Event A Event B
Event C 10 11
Event D 3 4
Event E 14 8
A) Determine the probability of P(CIA).
B) Determine the probability of P(BE).
C( Determine the probability of P(EB).

Answer 1

Explanation:

Hello!

The variable is

X: average mass of a sample of rocks collected in the waters of a region. (measured in grams)

Variables can be:

Quantitative: they represent number, any characteristic that can be "counted" is a quantitative variable, the most common examples are weight, volume, temperature, height, etc...

There are two types of quantitative variables:

⇒ Discrete variables: The only take certain values within the interval of definition of the variable, for example "number of sales" or "money in a wallet"

⇒ Continuous variables: They can take any value within an interval, in this example that you are working with mass, depending on the precision of the scale the mass can have infinite decimal values.

Qualitative: they represent characteristics that cannot be counted, meaning, they are not represented by numbers. There are many attributes that are qualitative variables, for example: colors, race of an animal, phenotypes, types of business, etc...

1)

The variable in this example is Quantitative, it takes numerical values, and the correct option is:

D. Quantitative, because numerical values, found by either measuring or counting, are used to describe the data.

2)

The values of mass of the rocks can take any value within the range of definition of the variable, they only depend on the precision of the scale used to weight the rocks.

B. Interval, because the differences in the data can be meaningfully measured, but the data do not have a true zero point.

3)

A standard 52-card deck contains 13 cards for each suit (clubs, diamonds, hearts and spades)

To calculate the probability of choosing a card at random and it being a Diamond, supposing that all cards are equally probable, you have to divide the total number of diamonds by the total number of cards in the deck:

P(diamond)= 13/52= 0.25

For items 4) and 5) the contingency tables are attached.

4)

a. and b. are conditional probabilities, to calculate them you have to apply the following formula:
`P(A|B)= (P(AnB))/(P(B))`

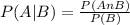
This means that the probability of the event "A" given that event "B" has occurred is equal to the probability of the intersection between events "A" and "B" divided by the probability of event "B"

a. P(A|C)=
`(P(AnC))/(P(C))`

To calculate the probability of the intersection P(A∩C) you have to divide the observations where both events cross by the total of observations on the table:

P(A∩C)= 10/50= 0.20

The probability of C is found in the margins of the table, in this case you have to divide the total of observations for event C by the total of observations of the table:

P(C)= 21/50= 0.42

Now you can calculate the asked probability:

`P(A|C)= (0.2)/(0.42)= 0.48`

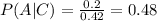
b. P(C|A)=
`(P(AnC))/(P(A))`

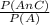
From item a. we already know that P(A∩C)= 10/50= 0.20

The probability of event A is in the margin of the table and you calculate it as:

P(A)= 27/50= 0.54

Then:

`P(C|A)= (0.20)/(0.54) = 0.37`

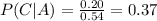
c. P(BE)

This symbolized the probability of the events "B" and "E" occurring at the same time, you can also symbolize it as P(B∩E)

To calculate the probability of B and E happening you have to do as follows:

P(B∩E)= 8/50= 0.16

5)

a. P(C|A)= 0.37 (As calculated in 4b.)

b. P(BE) and c. P(EB) ⇒ Both expressions symbolize the intersection between events "B" and "E", P(B∩E)= P(E∩B)= 0.16 (As calculated in 4c.)

I hope this helps!