Question

Use the Law of Sines to complete an expression that represents the angle measure x.

Answer 1

The length of a is equal to 14.9.

The angle measure of b is equal to 71°.

The length of c is equal to 25.5.

General Formulas and Concepts:
Pre-Calculus

Law of Sines:

`\displaystyle \bold{ (\sin A)/(a) = (\sin B)/(b) = (\sin C)/(c) }`

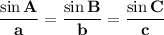
Explanation:

Step 1: Define

Identify given from triangle.

Length corresponding with x°: 14.9

Other given angle: 71°

Length corresponding with 71°: 25.5

Step 2: Find Values

1. [Law of Sines] Substitute in variables:
   
   `\displaystyle (\sin x^\circ)/(14.9) = (\sin 71^\circ)/(25.5)`
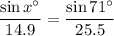
2. Isolate x° term:
   
   `\displaystyle \sin x^\circ = (14.9 \sin 71^\circ)/(25.5)`
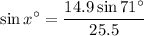
3. Isolate x°:
   
   `\displaystyle x^\circ = \sin^(-1) \bigg( (14.9 \sin 71^\circ)/(25.5) \bigg)`
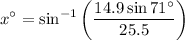
4. Identify variables:
   
   `\displaystyle a = 14.9 , \ b = 71^\circ , \ c = 25.5`

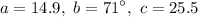
∴ we have completed the expression using Law of Sines.

---

Topic: Precalculus

Unit: Trigonometry