The 7th term of the geometric sequence is 1/2 or 0.5.
What is a a geometric sequence.
A geometric sequence is an array of numbers in which each term that follows the first term is determined by multiplying the previous term by the common ratio.
The general formula for the nth term of a geometric sequence can be expressed as:
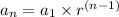
Given that:
The third term
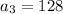 , and:
, and:
The common ratio
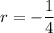
Then; the third term
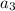 becomes;
becomes;
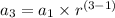
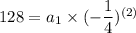
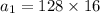

Now, the 7th term can be computed as:
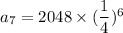
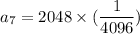
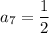
Therefore, the 7th term of the geometric sequence is 0.5.