Answer:
Option (2).
Explanation:
This question is incomplete; here is the complete question and find the figure attached.
In the diagram of a circle O, what is the measure of ∠ABC?
27°
54°
108°
120°
m(minor arc
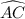 ) = 126°
) = 126°
m(major arc
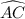 ) = 234°
) = 234°
By the intersecting tangents theorem,
If the two tangents of a circle intersect each other outside the circle, measure of angle formed between them is half the difference of the measures of the intercepted arcs.
m∠ABC =
![(1)/(2)[m(\text {major arc{AC})}-m(\text{minor arc} {AC})]](https://img.qammunity.org/2021/formulas/mathematics/high-school/4s8hdfy9xtkjmd32tn2hed5xhaiuevf9y2.png)
=
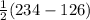
= 54°
Therefore, Option (2) will be the answer.