Answer:

The area is given by:
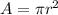
And replacing we got:
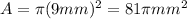
So then we can conclude that the area of the coin is
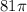 mm^2
mm^2
Explanation:
For this case we know that we have a coin with a diamter of
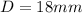 , and by definition the radius is given by:
, and by definition the radius is given by:

The area is given by:
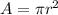
And replacing we got:
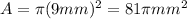
So then we can conclude that the area of the coin is
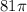 mm^2
mm^2