Question

An accident in a laboratory results in a room being contaminated by a radioisotope with a half life of 4.5 hours. If the radiation is measured to be 64 times the maximum permissible level, how much time must elapse before the room is safe to enter? The mass of Helium atom is 4.002602 u (where u = 1.66 x 10-27 kg) but the mass of 1 proton is 1.00730 u and 1 neutron is 1.00869 u. Calculate the binding energy per nucleon in MeV.

Answer 1

a) t = 27.00 h

b) B = 6.84 MeV/nucleon

Step-by-step explanation:

a) The time can be calculated using the following equation:

`R = R_(0)e^(-\lambda*t)`

Where:

R: is the radiation measured at time t

R₀: is the initial radiation

λ: is the decay constant

t: is the time

The decay constant can be calculated as follows:

`t_(1/2) = (ln(2))/(\lambda)`

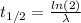
Where:

t(1/2): is the half life = 4.5 h

`\lambda = (ln(2))/(t_(1/2)) = (ln(2))/(4.5 h) = 0.154 h^(-1)`

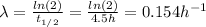
We have that the radiation measured is 64 times the maximum permissible level, thus R₀ = 64R:

`(R)/(64R) = e^(-\lambda*t)`

`t = -(ln(1/64))/(\lambda) = -(ln(1/64))/(0.154 h^(-1)) = 27.00 h`

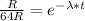
b) The binding energy (B) can be calculated using the following equation:

`B = ((Z*m_(p) + N*m_(n) - M_(A)))/(A)*931.49 MeV/u`

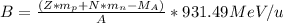
Where:

Z: is the number of protons = 2 (for
`^(4)_(2)He`)

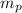`m_(p)`: is the proton mass = 1.00730 u

N: is the number of neutrons = 2 (for
`^(4)_(2)He`)

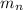`m_(n)`: is the neutron mass = 1.00869 u

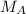`M_(A)`: is the mass of the He atom = 4.002602 u

A = N + Z = 2 + 2 = 4

The binding energy of
`^(4)_(2)He` is:

`B = ((2*1.00730 + 2*1.00869 - 4.002602))/(4)*931.49 MeV/u = 7.35\cdot 10^(-3) u*931.49 MeV/u = 6.84 MeV/nucleon`

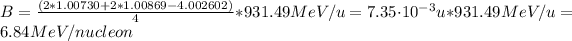
Hence, the binding energy per nucleon is 6.84 MeV.

I hope it helps you!