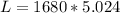Question

A woman with mass 50 kg is standing on the rim of a large disk that is rotating at 0.80 rev/s about an axis through its center. The disk has mass 110 kg and radius 4.0 m. Calculate the magnitude of the total angular momentum of the woman–disk system. (Assume that you can treat the woman as a point.)

Answer 1

The angular momentum is
`L = 8440.32 \ kg \cdot m^2 \cdot s^(-1)`

Step-by-step explanation:

From the question we are told that

The mass of the woman is
`m = 50 \ kg`

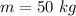
The angular speed of the rim is
`w = 0.80 \ rev/s = 0.8 * [(2 \pi)/(1) ] = 5.024 \ rad \cdot s^(-1)`

The mass of the disk is
`m_d = 110 \ kg`

The radius of the disk is
`r_d = 4.0 \ m`

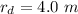
The moment of inertia of the disk is mathematically represented as

`I_D = (1)/(2) m_d r^2_d`

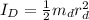
substituting values

`I_D = (1)/(2) * 110 * 4^2`

`I_D = 880 \ kg \cdot m^2`

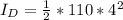
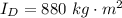
The moment of inertia of the woman is

`I_w = m * r_d^2`

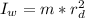
substituting values

`I_w = 50 * 4^2`

`I_w =800\ kg`

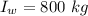
The moment of inertia of the system (the woman + the large disk ) is

`I_t = I_w + I_D`

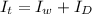
substituting values

`I_t = 880 +800`

`I_t =1680 \ kg \cdot m^2`

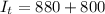
The angular momentum of the system is

`L = I_t w`

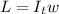
substituting values

`L = 1680 * 5.024`

`L = 8440.32 \ kg \cdot m^2 \cdot s^(-1)`