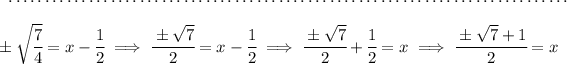Question

Determine the next step for solving the quadratic equation by completing the square.

0 = –2x2 + 2x + 3
–3 = –2x2 + 2x
–3 = –2(x2 – x)
–3 +
= –2(x2 – x + )
StartFraction negative 7 Over 2 EndFraction = –2(x – StartFraction 1 Over 2 EndFraction)2
StartFraction 7 Over 4 EndFraction = (x – StartFraction 1 Over 2 EndFraction)2
The two solutions are
Plus or minus StartFraction StartRoot 7 EndRoot Over 2 EndFraction.

Answer 1

see picture

Explanation:

-1/2
1/4
1/2

Answer 2

`\qquad \textit{perfect square trinomial} \\\\ (a\pm b)^2\implies a^2\pm \stackrel{\stackrel{\text{\small 2}\cdot \sqrt{\textit{\small a}^2}\cdot \sqrt{\textit{\small b}^2}}{\downarrow }}{2ab} + b^2`

the idea behind the completion of the square is simply using a perfect square trinomial, hmmm usually we do that by using our very good friend Mr Zero, 0.

if we look at the 2nd step, we have a group as x² - x, hmmm so we need a third element, which will be squared.

keeping in mind that the middle term of the perfect square trinomial is simply the product of the roots of "a" and "b", so in this case the middle term is "-x", and the 1st term is x², so we can say that

`\stackrel{middle~term}{2(√(x^2))(√(b^2))~}~ = ~~\stackrel{middle~term}{-x}\implies 2xb~~ = ~~~~ = ~~-x \\\\\\ b=\cfrac{-x}{2x} \implies b=-\cfrac{1}{2}`

so that means that our missing third term for a perfect square trinomial is simply 1/2, now we'll go to our good friend Mr Zero, if we add (1/2)², we have to also subtract (1/2)², because all we're really doing is borrowing from Zero, so we'll be including then +(1/2)² and -(1/2)², keeping in mind that 1/4 - 1/4 = 0, so let's do that.

`-3~~ = ~~-2\left[ x^2-x+\left( \cfrac{1}{2} \right)^2 ~~ - ~~\left( \cfrac{1}{2} \right)^2\right]\implies -3=-2\left(x^2-x+\cfrac{1}{4}-\cfrac{1}{4} \right) \\\\\\ -3=-2\left(x^2-x+\cfrac{1}{4} \right)+(-2)-\cfrac{1}{4}\implies -3=-2\left(x^2-x+\cfrac{1}{4} \right)+\cfrac{1}{2} \\\\\\ -3-\cfrac{1}{2}=-2\left(x^2-x+\cfrac{1}{4} \right)\implies -\cfrac{7}{2}=-2\left(x-\cfrac{1}{2} \right)^2\implies \cfrac{7}{4}=\left(x-\cfrac{1}{2} \right)^2`

`~\dotfill\\\\ \pm\sqrt{\cfrac{7}{4}}=x-\cfrac{1}{2}\implies \cfrac{\pm√(7)}{2}=x-\cfrac{1}{2}\implies \cfrac{\pm√(7)}{2}+\cfrac{1}{2}=x \implies \cfrac{\pm√(7)+1}{2}=x`