Answer:
After 1st year, the age distribution will be
![x_1 = \left[\begin{array}{ccc}1584\\36\\108\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/8czo7h9arhoboj9ss471jb9g2r0e1jt7u1.png)
After 2nd year, the age distribution will be
![x_2 = \left[\begin{array}{ccc}5256\\396\\27\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/if4jn34yosxvrxq40nl0mfg1h6a6ylrer4.png)
Explanation:
A population has the following characteristics.
A total of 25% of the population survives the first year. Of that 25%, 75% survives the second year.
The average number of offspring for each member of the population is 3 the first year, 5 the second year, and 3 the third year.
From the above information, we can construct a transition age matrix.
![A = \left[\begin{array}{ccc}3&5&3\\0.25&0&0\\0&0.75&0\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/qxib6pytwgkqyfor2l9z6x8l4rhppm92ej.png)
The population now consists of 144 members in each of the three age classes.
From the above information, we can construct the current age matrix.
![x = \left[\begin{array}{ccc}144\\144\\144\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/bx77itjf0piq0suk71d3d4tlfok0i08g0a.png)
How many members will there be in each age class in 1 year?
After 1st year, the age distribution will be
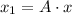
![x_1 = \left[\begin{array}{ccc}3&5&3\\0.25&0&0\\0&0.75&0\end{array}\right] * \left[\begin{array}{ccc}144\\144\\144\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/rqbcru8fv5j3ym05ap3wc1mqbmz9warirt.png)
The matrix multiplication is possible since the number of columns of first matrix is equal to the number of rows of second matrix.
![x_1 = \left[\begin{array}{ccc}1584\\36\\108\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/8czo7h9arhoboj9ss471jb9g2r0e1jt7u1.png)
After 2nd year, the age distribution will be
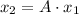
![x_2 = \left[\begin{array}{ccc}3&5&3\\0.25&0&0\\0&0.75&0\end{array}\right] * \left[\begin{array}{ccc}1584\\36\\108\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/99g2aak5jxa6t5v6l466evfj16c4hdqk3d.png)
![x_2 = \left[\begin{array}{ccc}5256\\396\\27\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/if4jn34yosxvrxq40nl0mfg1h6a6ylrer4.png)