Question

A comparison is made between two bus lines to determine if arrival times of their regular buses from Denver to Durango are off schedule by the same amount of time. For 51 randomly selected runs, bus line A was observed to be off schedule an average time of 53 minutes, with standard deviation 17 minutes. For 60 randomly selected runs, bus line B was observed to be off schedule an average of 60 minutes, with standard deviation 13 minutes. Do the data indicate a significant difference in average off-schedule times? Use a 5% level of significance.

a. Level of significance, null and alternative hypothesis
b. What sampling distribution will you use? What assumptions are you making? What is the value of the sample test statistic?
c. Find or estimate the P-value
d. Based on your answers to part a and c will you reject or fail to reject the null hypothesis? Are the data statistically significant at level alpha?
e. Interpret your conclusion in the context of the application

Answer 1

a) Level of significance α=0.05

Two-tailed test, with null and alternative hypothesis:

`H_0: \mu_1-\mu_2=0\\\\H_a:\mu_1-\mu_2\\eq 0`

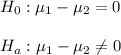
b) Student's t distribution. We assume equal variances for both populations, independent sampled values and populations normally distributed.

Test statistic t=-2.4

c) P-value = 0.018

d) Rejection of the null hypothesis.

The data is statistically significant.

e) There is evidence to conclude there is significant difference in average off-schedule times between the bus lines. The difference we see in the samples seems not due to pure chance.

Explanation:

This is a hypothesis test for the difference between populations means.

The claim is that there is a significant difference in average off-schedule times for this bus lines.

Then, the null and alternative hypothesis are:

`H_0: \mu_1-\mu_2=0\\\\H_a:\mu_1-\mu_2\\eq 0`

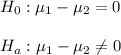
The significance level is 0.05.

The sample 1 (bus line A), of size n1=51 has a mean of 53 and a standard deviation of 17.

The sample 2 (bus line B), of size n2=60 has a mean of 60 and a standard deviation of 13.

The difference between sample means is Md=-7.

`M_d=M_1-M_2=53-60=-7`

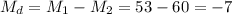
The estimated standard error of the difference between means is computed using the formula:

`s_(M_d)=\sqrt{(\sigma_1^2)/(n_1)+(\sigma_2^2)/(n_2)}=\sqrt{(17^2)/(51)+(13^2)/(60)}\\\\\\s_(M_d)=√(5.667+2.817)=√(8.483)=2.913`

Then, we can calculate the t-statistic as:

`t=(M_d-(\mu_1-\mu_2))/(s_(M_d))=(-7-0)/(2.913)=(-7)/(2.913)=-2.4`

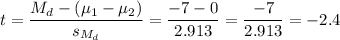
The degrees of freedom for this test are:

`df=n_1+n_2-1=51+60-2=109`

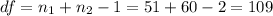
This test is a two-tailed test, with 109 degrees of freedom and t=-2.4, so the P-value for this test is calculated as (using a t-table):

`\text{P-value}=2\cdot P(t<-2.4)=0.018`

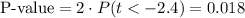
As the P-value (0.018) is smaller than the significance level (0.05), the effect is significant.

The null hypothesis is rejected.

There is enough evidence to support the claim that there is a significant difference in average off-schedule times for this bus lines.