Answer:
a)
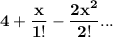
b) See Below for proper explanation
Explanation:
a) The objective here is to Use the power series expansions for ex, sin x, cos x, and geometric series to find the first three nonzero terms in the power series expansion of the given function.
The function is
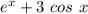
The expansion is of
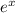 is
is
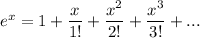
The expansion of cos x is
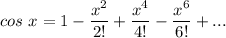
Therefore;
![e^x + 3 \ cos \ x = 1 + (x)/(1!)+ (x^2)/(2!)+ (x^3)/(3!) + ... 3[1 - (x^2)/(2!)+ (x^4)/(4!)- (x^6)/(6!)+ ...]](https://img.qammunity.org/2021/formulas/mathematics/college/mbusdpdkeg9s3l06ozicko85rjlcicllub.png)
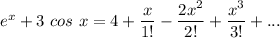
Thus, the first three terms of the above series are:
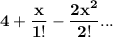
b)
The series for
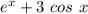 is
is
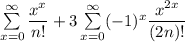
let consider the series;
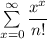
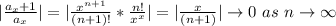
Thus it converges for all value of x
Let also consider the series
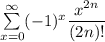
It also converges for all values of x