Answer:
I would need the radius of the cone to answer this completely, bit I can get you super close and explain it.
Explanation:
The formula for a cone is
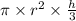
From there, I started plugging in numbers. I set this equation equal to 540pi because both if them are the volume, so they are equal and I simplified as much as I could from there. First off, the pi cancel each other out since they're on both sides of the equation. From there you have this equation:

Then, I multiplied both sides by 3 to get rid of the fraction on the left side of the equation:
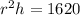
Finally, I got rid of the "squared" by putting a square root over both sides if the equation, getting this:
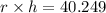
If I knew the radius. I could get the answer by dividing both sides by the radius.
Good luck!