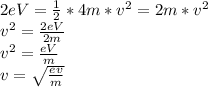Question

A helium ion of mass 4m and charge 2e is accelerated from rest through a potential difference V in vacuum. Its final speed will be

​

Answer 1

`v=\sqrt{(ev)/(m) }`

Step-by-step explanation:

The helium ion has:

a potential difference in vacuum = V,

Charge = 2e

and mass = 4m,

speed = v,

mass = 4m

From electrostatics, the work done is the product of charge and its potential difference.

Therefore, Work done = charge × potential difference = 2e × V = 2eV

This work done is in form of kinetic energy, therefore:

Kinetic energy = 1/2 × mass × speed²

⇒ Work done = Kinetic energy

`2eV=(1)/(2) *4m*v^2=2m*v^2\\v^2=(2eV)/(2m)\\ v^2=(eV)/(m)\\ v=\sqrt{(ev)/(m) }`