Question

What should be added in the polynomial x3-6x2+11x+8 so that it is completely divisible by 1-3x +x2

Answer 1

The value to be added to the polynomial x³ - 6·x² + 11·x + 8 so that it is completely divisible by 1 - 3·x + x² is -(x + 11)

Explanation:

By long division, we have;

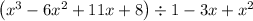`{\left ({x^(3)-6x^(2)+11x+8} \right )/ 1 - 3x + x^(2)}` = x - 3

-(x³ - 3·x² + x)

-3·x² + 10·x + 8

-(-3·x² + 9·x -3)

x + 11

Therefore, -(x + 11) should be added to the polynomial x³ - 6·x² + 11·x + 8 so that it is completely divisible by 1 - 3·x + x².

That is (x³ - 6·x² + 11·x + 8 - x - 11) ÷ (1 - 3·x + x²) = x - 3.