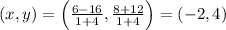Answer:
Coordinates of M =
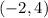
Explanation:
Given: AM:MB = 1:4, A has coordinates (-4, 3) and B has coordinates (6, 8)
To find: coordinates of M
Solution:
According to section formula, if M(x, y) divides line joining points
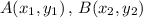 in ratio
in ratio
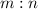 then coordinates of point M are
then coordinates of point M are
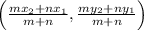
Put
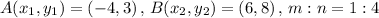
Therefore,